学習塾ブランチの西原です。
今月は定期試験の月ですね!前期期末(2学期中間)のリベンジに燃えている子ども達も多いと思います。
今日は中1の球の表面積と体積について
学校によってはテスト範囲に入ってくるかもしれませんので、要チェックです!

球の表面積と体積の公式
まずは公式を確認しましょう。
球の表面積、体積は覚えにくい上に、この単元以降は一切出てきません。
そのため、中3になる頃にはほとんどの生徒が忘れてしまい、模試で急に出題されて焦ってしまう問題の一つです。
まずは表面積と体積の公式を確認しましょう。
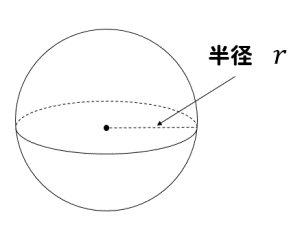

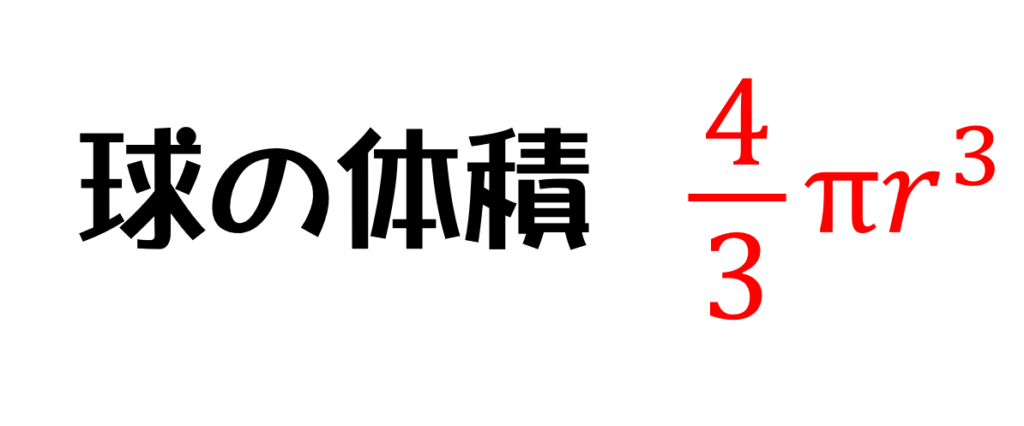
「しんぱいあるある」と語呂合わせで覚えている方も多いかもしれませんが、その語呂合わせすら忘れてしまうほど中1以降は扱いません。
今日は別のアプローチをしたいと思います。
球の表面積
まずは球の表面積
表面積はシンプルに
球の表面積=円の面積の4倍
と覚えましょう。
半径rの円の面積はr×r×π つまり πr2。 これに×4をしたのが球の表面積4πr2です。
公式を覚えるだけならこれでOKですが、もう少ししっかり理解したいという方は
こちらの動画が非常に分かりやすいのでお勧めです。
球の体積
つづいて、球の体積です。
証明をするとなる微積が必要ですが、中学生に教えるには微積は使えません。
もっと直感的なアプローチをしましょう。
この写真をみてください。

紙コップを集めて球体を作っています。この紙コップは円錐を切った形をしています。
紙コップの底が円錐状になっているものを想像してください。
つまり球というのは、錐形の集合体と考えることもできます。
錐の体積は低面積×高さ×1/3でしたね。
この公式は球の体積にも使えます。
低面積は球の表面積のことです。
高さは円の半径rです。つまり、
球の体積=球の表面積(4πr2)×高さ(r)×1/3
となります。
これを計算すると3/4πr2の式が出てきます。
円の面積や錐の体積は覚えられている生徒が多いですので、
この形だと覚えやすく思い出しやすいと思いますので、是非試してみてください。

